Зачем нужна математика и как она помогает выходить из сложных ситуаций

Уравнения и формулы знакомы нам по школьным урокам математики, физики и химии. Но у большинства людей они стираются из памяти почти сразу после экзаменов. И это логично: в повседневной жизни нам требуются лишь простейшие арифметические действия или калькулятор на телефоне.

Но на самом деле формулы необходимы. Ведь абсолютно все — от образования галактик до расположения веснушек на носу — есть результат решения уравнений. Возможно, это достаточно веская причина познакомиться с математикой поближе. Предлагаем начать с задачи о том, как спастись от песчаной бури и сохранить важные для человечества ископаемые из книги «Формулы на все случаи жизни».

Недели раскопок под палящим солнцем Сахары наконец-то окупились: ваша команда обнаружила окаменелые кости доисторического гоминида, что может перевернуть общепринятые представления об эволюции человека. Запасы еды и воды тем временем подходят к концу, да и сама мать-природа явно готовится бросить вызов: согласно метеопрогнозу, ожидается мощнейшая песчаная буря. Нужно срочно эвакуироваться, но место такое удаленное, что выбраться можно только пешком или верхом на верблюде.

Оставлять находки не стоит: если их забыть — случайно или намеренно, — они будут погребены под слоем песка. Местные жители, разумеется, перевозят тюки с грузом отнюдь не бесплатно и, следуя давней традиции, рассчитывают стоимость услуг по максимальному измерению ящика (длине, ширине или высоте), при этом 1 см = 1 дирхаму. Строение обнаруженной при раскопках os femoris (выражаясь простым языком, бедренной кости) свидетельствует о бипедализме — двуногости — древнего гоминида. Находку длиной 40 см надлежит взять с собой, но у вас всего 35 дирхамов. Сможете ли вы, используя свои познания в геометрии, упаковать кость так, чтобы и сэкономить на транспортировке, и успеть до того, как местность накроет песчаная буря?

Навыки эффективной упаковки вещей необычайно полезны в нынешних реалиях — и не только потому, что большинство авиакомпаний устанавливают до обидного низкие нормы провоза багажа. Владение этими навыками упрощает перевозку крупных корабельных, а также средних и мелких грузов. (Когда я писал эту главу, математический алгоритм, который помогал бы оптимизировать размещение вещей в багажном отсеке фургона, все еще не был придуман. Сумеете разработать требуемую последовательность действий — сорвете куш и войдете в историю.) Тем не менее, когда необходимо положить в ящик нечто прямое и продолговатое, всегда обращаются к знаменитой теореме Пифагора. Ее помнят почти все (а если кто-то и подзабыл, то в начале книги приведена краткая справка), но известно ли вам, что существует ее трехмерная версия? Таковая весьма полезна при необходимости упаковать прямую продолговатую кость в ящик с более короткими сторонами. Звучит невероятно, но давайте обдумаем проблему и выясним, каким образом длинная палка способна поместиться в таре заданных размеров.

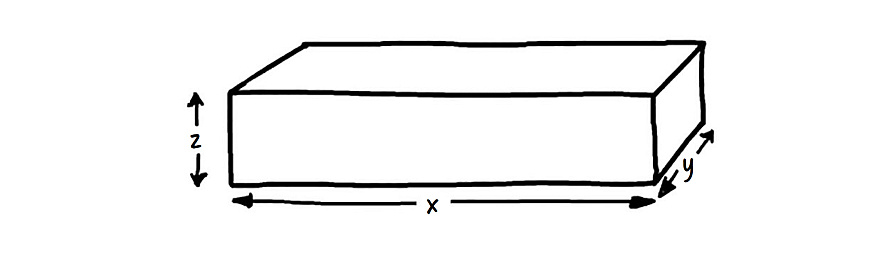
Предположим, что ящик представляет собой кубоид (прямоугольный параллелепипед) размерами x метров на y метров на z метров. Чтобы определить длину диагонали, помеченную как d, придерживайтесь более простой, двухмерной, версии теоремы Пифагора:

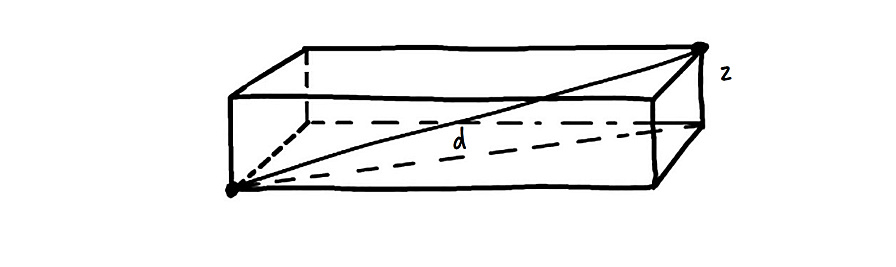
Вам нужны две из трех сторон треугольника, но на данный момент известна всего одна — высота ящика, она же z. Тем не менее, применив все ту же теорему Пифагора, вы можете вычислить длину отрезка, который по диагонали пересекает дно ящика:

Согласно Пифагору, длина этого отрезка должна быть вот такой:

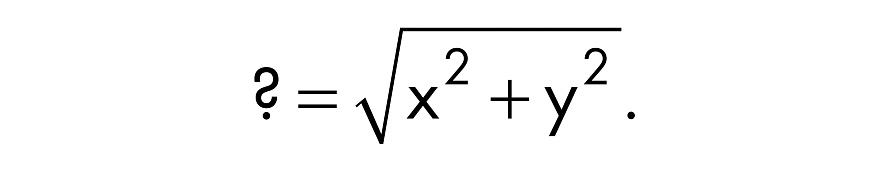
Возведите в квадрат обе стороны уравнения (зачем, поймете через минуту):

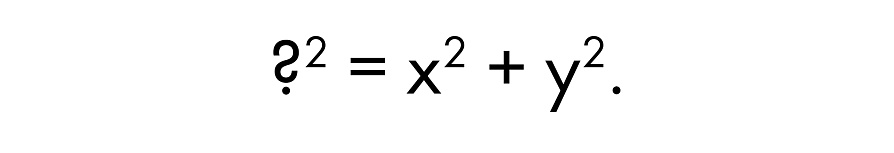
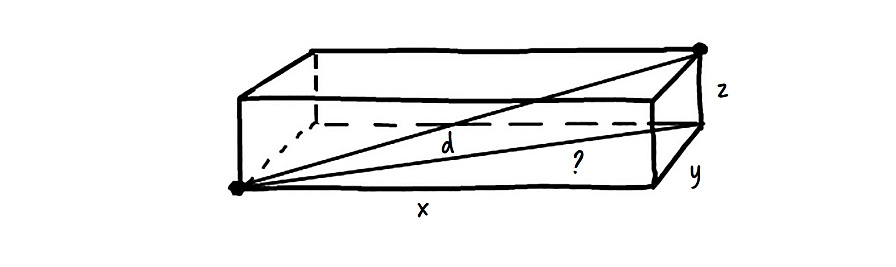
Вернитесь к исходному треугольнику:

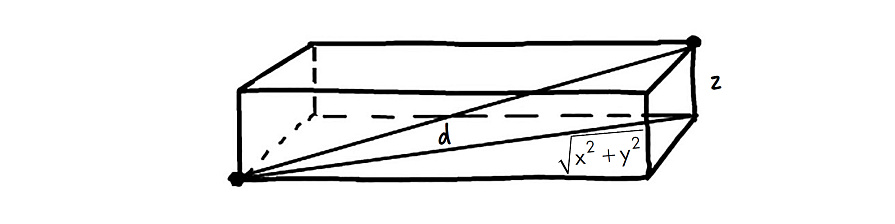
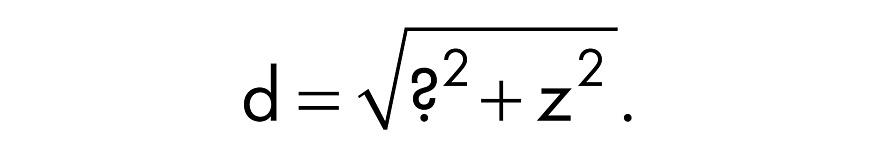
Теперь вам очевидно, зачем понадобилось выражение для отрезка, обозначенного вопросительным знаком? Подставив его значение, получите:

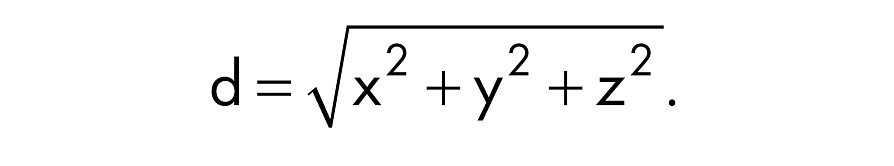
Поскольку для обозначения сторон своей тары вы использовали переменные, это уравнение — трехмерная версия теоремы Пифагора — подойдет для абсолютно любого ящика.

Давайте вернемся в Сахару. Буря еще далеко, однако на горизонте уже виднеется пылевое облако, и совсем скоро оно подберется к лагерю. Очевидно, что время уходит. Подыскивая тару для бесценной находки, вы решаете упаковать кость в ящик кубической формы, то есть со сторонами одинаковой длины. Поскольку плату с вас все равно возьмут в соответствии с самой длинной стороной, все остальные размеры могут быть точно такими же. Иначе вы заплатите ту же сумму при меньшем d. Итак, если все грани имеют равную длину, то y и z совпадают с x. Замените y и z в формуле на x:

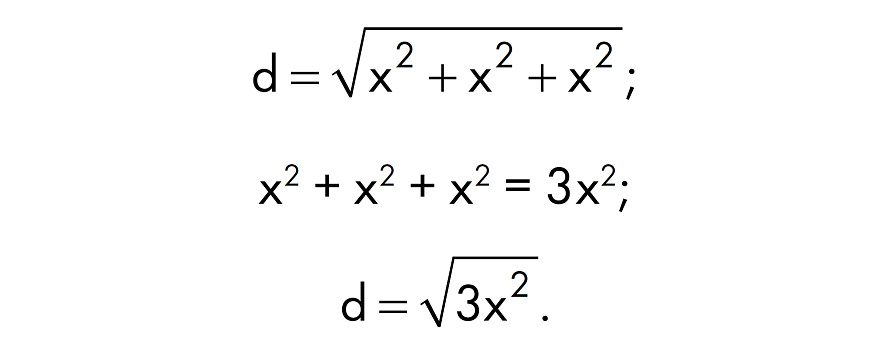
Квадратный корень из 3×2 равен квадратному корню из 3, умноженному на квадратный корень из x2:

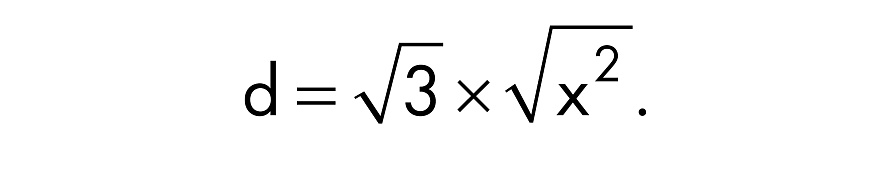
Вы помните, что квадрат и квадратный корень — обратные операции. Значит, они успешно отменяют друг друга:

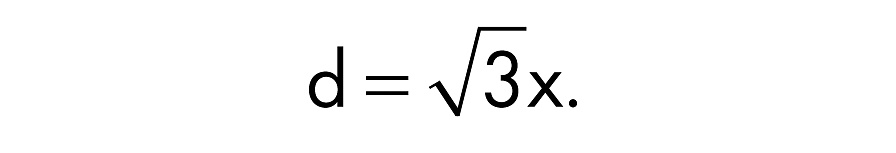
Уравнение показывает, что диагональ куба в 3 раза больше его стороны. Поскольку 3 с округлением до двух знаков после запятой равен 1,73, в кубический ящик получается поместить нечто на 73% длиннее его грани. Преобразуйте формулу, разделив обе части на 3, что даст следующее:

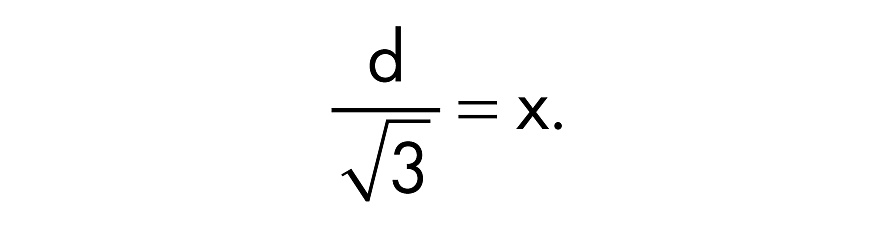
Бедренная кость имеет длину 40 см:

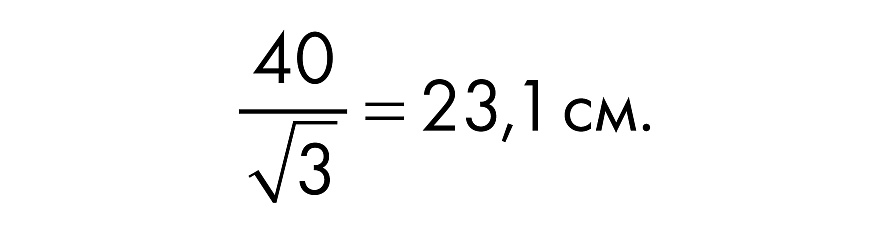
Настоящая бедренная кость толще теоретической прямой, поэтому возьмите тару чуть больше. Теперь вы уверились в истинности утверждения «мал золотник, да дорог»? Между гранями ящика и бедренной костью остается свободное пространство, куда удается упаковать еще пару-тройку обнаруженных вами мелких костей. Вы раздаете остатки денег членам команды и, прежде чем отправиться в путь пешком, наблюдаете, как нагруженный верблюд скрывается в лучах заходящего солнца.

Рекомендуем книгу